목차
- 공변(covariant) & 반변(contravariant)이란?
- 왜 사용하는가?
- 쌍대 공간 (dual space)
- 활용 가능성
1. 공변(covariant) 벡터 & 반변(contravariant) 벡터란?
공변 벡터와 반변 벡터는 기하학적으로 물리적 대상을 기술하는 방법에 있어
기저(basis)가 변화할 때의 변화를 설명한다.
- 말이 어렵게 느껴질 수 있지만 밑에까지 읽고 온뒤 다시 본다면 이해할 수 있을 것이다.
covariant에서 co는 기저벡터의 증가에 따라 공변 성분이 같이 증가하기 때문이다.
contravariant에서 contra는 기저벡터의 증가에 따라 반변 성분이 감소하기 때문이다.

◎그림 설명 :
1. contravariant는 기저 벡터가 증가하면 A^2(index) 값이 작아진다.
2. covariant는 기저 벡터가 증가하면 A_2(index) 값이 증가한다.
자 여기까지는 일반 블로그에서 알려주는 공변과 반변에 대한 대략적인 설명이다.
자 그러면 지금부터 이해할 수 있는 방법에 대해 알아보자~~♪
contravariant vector를 화살표라고 생각하고 covariant vector를 스텍(grid)이라고 생각해보자
contravariant vector |
covariant vector |
 |
|
"# stacks pierced by vector"은 covariant vector와 contravariant vector가 곱해졌을 때 scalar 값이 된다는
사실을 인지하고 넘어가면 된다.
위와 같이 예를 들면 굉장히 이해되기 쉬울 것이다.
ex1) covariant vector는 grid이기 때문에 기저벡터를 늘린다는 뜻은 grid의 칸이 밀해진다는 뜻과 같다. 그렇기에 grid가 밀해지면 통과하는 벡터의 값은 늘어나게 될 것이다.
ex2) contravariant vector는 여러분이 아시는 그게 맞다. 간단한 예시를 들어보자 (4, 4)의 점이 있다. (기저벡터가 1일 때) 이 때 기저 벡터가 2가 되면 (2, 2)로 옮겨질 것이다. 그렇기 때문에 작아진다. - 너무 당연한 말,,,,
참고로 이 설명을 하는 블로그를 본 적이 없다. 위의 사실을 이해했다면 왠만한 사람보다는 직관적인 의미를 더 확실하게 아는 것이다.

2. 왜 사용하는가?

유감스럽게도 우리 우주는 평평하지 않다.
한 번쯤 보고 들어봤을 것이다. (행성의 공전을 설명하기 위해 천 위에 무거운 추를 올려놓고 그 주위로 구슬을 굴리는 것을)

이 부분에서 문제가 생긴다. 중력은 시공간의 왜곡을 야기한다.
이로인해 모두의 좌표계가 평평하지 않아 모두가 평평한 좌표계를 사용한다면 어디에서 측정하는가에 따라 값이 달라질 것이다.
그렇기 때문에 우리가 공변과 반변을 학습하는 것이다.
** 이해하기 어려운 사람들이 있을까봐!!**
- covariant vector와 contravariant vector가 곱해지면 스칼라가 나온다고 했다. <<위의 그림 참조>>
- (내가 노트북의 길이를 자로 지구에서 측정한 것과 안드로메다 은하에서 측정한 값은 같다.)
- 중요성은 우리가 속한 우주 어느곳에서든 반변과 공변을 이용한다면 똑같은 결과가 도출되게 유도할 수 있다는 뜻이다.
(사실상 위에 설명한 한 줄이 가장 중요하다!!!)
반변과 공변이 무엇인지 궁금했던 사람은 여기까지 보면된다.
3. 쌍대 공간 (dual space)
우선 dual space가 갑자기 뭐냐?? 라는 질문이 생길 수 있다.
사실 dual vector가 covariant다....
원래 공부를 하다보면 하나의 뜻을 굉장히 다양하게 표현하는 것을 볼 수 있을 것이다.
Ex) 하나의 뜻을 다양하게 표현한 예시
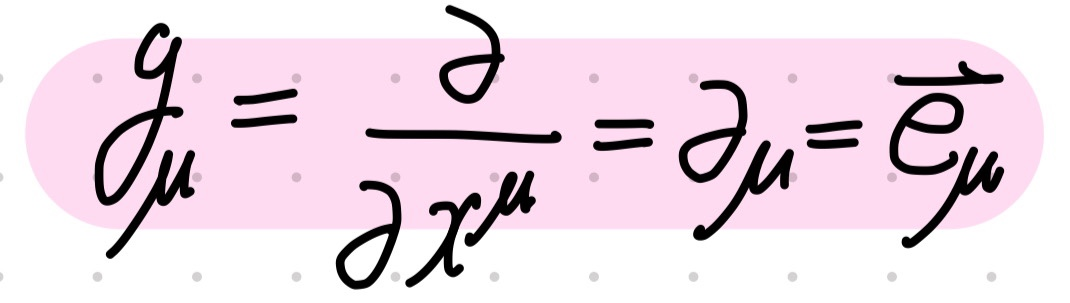
지금 여러분이 알아두셔야 할 것
1. covariant = dual vector
2. contravariant = vector
쌍대공간의 엄밀한 정의
- 벡터 공간 V가 주어지면, 그 위의 쌍대공간 V^*은 V에서 기저 체(스칼라)로 가는 모든 선형 함수들의 집합
(전에 화살표가 grid를 얼마나 꽤뚫는지로 예시를 들어줬는데 그것을 생각하면 된다.)
- 즉, V^*의 원소는 V위의 선형 사상이다.

쌍대곱셈 : 쌍대공간의 원소와 벡터공간의 원소를 곱해 스칼라를 반환하는 연산

여러분 : 아니......tlakf 이게 뭔 ro소리야??
나 : 일단 진정하고 조금만 기다려라
선형사상(linear map)란?
선형사상(linear map)은 두 벡터공간 사이에 정의되는 사상 가운데 벡터공간의 성질을 보존하는, 즉 선형성을 갖는 함수를 말한다. 선형변환(linear transform) 이라고도 한다.
두 벡터공간 V와 W에 대하여 선형사상 f : V -> W 라고 하면, 다음 조건을 만족하는 사상이다.
(벡터 합, 스칼라 곱 조건)
1. 벡터의 합 조건 : f(v_1+v_2) = f(v_1) + f(v_2)
2. 스칼라 곱 조건 : f(cv) = cf(v), 단 c is arbitrary real number
체(Field) 란?

**@@ 헷갈리지 말아라 @@**
이 field는 중력장의 장과는 다른 field다.
**아벨군
교환법칙을 만족하는 군이다. (그냥 교환법칙해도 되는 것들)
쉽게 설명하자면 다음과 같다 덧셈과 곱셈이 모두 가능하고 교환법칙이 성립하는 '것'들이다. (곱셈 부분에서 0은 제외)
환(Ring) 이란? - 궁금한 사람이 있을까봐,, (몰라도 된다.)

4. 활용가능성
1. 모든 곳
말 그대로 안 쓰이는 곳이 없다. 전자기력, 약력, 강력, 중력, 양자역학(spin), 입자물리학, 라그랑주 밀도 등....
다음 챕터는 공변 미분이다.
중력장 방정식을 이해하는 그날까지 화이팅이다!!

'중력장 방정식 - 아인슈타인(일반 상대성 이론)' 카테고리의 다른 글
| 크리스토펠 기호 (Christoffel symbol) - 중력장 방정식 (0) | 2025.03.24 |
|---|---|
| 레비치비타 커넥션 (Levi-Civita connection) - 중력장 방정식 (0) | 2025.03.24 |
| 공변 미분 (covariant derivative) - 중력장 방정식 (1) | 2025.03.24 |